SENSE隨筆131108
人機之辨
A字人執筆
〈阿蟬楔子〉
《Gödel,Escher,Bach》是一本七百多頁,意圖以數學、邏輯和對稱性等角度去解釋意識如何產生的著作。 人到底是如何由無意義的分子結構演變成有意義,擁有自我意識,把自身稱呼為“我”的人物呢?
誠如作者Hofstadter接受《Wired》雜誌訪問時指出,絕大部分的讀者並沒有認真看待他的意圖,反倒是將注意力放在幽默的細節上面。 我雖沒讀過這書,但單在Youtube上看麻省理工為此書製作給中學生的入門介紹,也已頭暈眼花,不得不佩服A字兄的過人膽識和毅力。
人在追逐知識的過程中,發明了一種方法,便是按照想要描述的 對象群 建立一個 對應系統,並以系統的規則代表該對象群運作的法則:那麼,「對象」和「系統」便成為同構的isomorphic事物。***
數學中的「 形式系統formal system」可算是此類知識系統的極致。***
若以邏輯推理為例去鬆散定義形式系統,它的原素應包括:
- 符號symbol:建立邏輯句子的可用符號;
- 語法grammar:決定何為合式well-formed句子的規則;
- 公設axiom:推理的起點(不證自明的);
- 推理規則rule of inference:按照 “前提premise”提供 “結論conclusion”的規則。
若系統包括以上諸原素,則以公設為起點,按照推理規則,以符號和語法推導出的結論,便稱為 「定理theorem」。***
〈A字人文章〉
MU謎語
電腦編製的課程中常以 「圖靈機器Turing machine」為原始電腦的教學例子,其中一個變種為「字串改動機器string manipulation machine」。
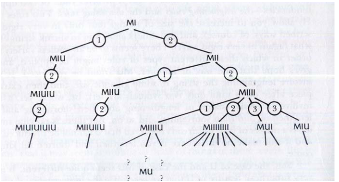
舉例:現時有一個系統,它可用的符號只有M、U和I,而系統只能辨認連續排列的符號。
課題: 系統開始時的字串為 MI,試按以下四項規則,將字串改動成為 MU。***
規則:
- 如果字串最後的符號為I,可以在後面加上U
舉例:字串MI可以改寫為MIU。 - 可將任何M以後的字串重覆
舉例:MIU可以變為MIUIU;MI可以變為MII。 - 可以U取代任何III
舉例:MIIII可以變為MUI,或MIU。 - 可刪除任何的UU
舉例:如MUUI可改寫為MI。
趁閣下運算的時候,且說一下其他。
一般人開始字串改動的時候,會先隨意探索,變動字串,慢慢地他會發現變動之間有共通之處,那麼他就開始創造新的規則,然後以自己的規則改寫字串,以圖達標。
另一方面,機器一開始就會不停運算直至海枯石爛,但一個人對著複雜的問題可能會覺得無法解決而內心抱怨。
人就是不能停止反思自身所做的事***,反思 [ 反思自身所做的事 ] 的事…..如此類推。
人的另一個特質就是會停止工作程序。***
例如筆者看此書時會跳去看facebook,回覆whatsapp,或者單純是看得太久很悶不看了。一部下棋的機器,你教曉它所有的規則,並不能令它意識到它在 “下棋系統”之中,更遑論擲棋不下離開這個系統了。
言歸正傳:
處理這類問題其中一個最直觀的方法,便是 「試誤法trial and error」。*** 像嘗試將魔方(扭計骰)還原一樣,雖然有效的方法相當多,但盲目地試誤是可以得到 “解solution”的。 “解”其實是公設,即遊戲的起點。
“MU謎語” 的問題是我們無法知道MU是否真的可以達到。***
若按照遊戲的條件,即以MI為起點,將任何適用的規則加在當前的字串上,並繪制一幅「樹枝圖tree diagram」,是否可以找出MU這個解呢?
應用以上的方法去測試結果的真偽有點荒謬,因為需要接近無限的時間來進行運算。***
“測試”需要在有限的時間完成才有意義。 測驗一個形式系統是否能得出個別定理時,必須找出一種「演算法algorithm」去確認該推理是否有決定性decisive,這個尋找合適演算法的過程稱為「決定性程序 decision procedure」***。有了決定性程序就能夠掌握系統結果,即theorem的特質,並且可以排除所有不可能的組合。
謎底〈無解的MU謎題〉
- MU字串的嘗試得到的結果是MU,即在推理過程中必須將I去除;
- 系統的規則 (3)是唯一可以去除I的規則,但若要完全去除I,I的數量必須能整除以3;
- 遊戲的起始字串是MI,即有1個I,而規則(2)是唯一能將I增加的規則,而每次只能增。2 x n不能整除以3,故I在字串中永遠無法去除。****
形式系統能夠反映一部份的現實嗎? 可以製造能反映現實的系統嗎? 還是現實就是一套形式系統? 以粒子的存在運作,命題是”時間的開始”,這就觸及宇宙決定論的問題。
說起「人工智能」,由未來戰士電影中擁有情感的機械人,到電飯鍋感應米水比例的功能都稱為人工智能,究竟人和機器的界限在哪裡? 我們可以製造一部能思考的機器嗎? 能否以數學形式為機器訂立規條以進行 “思考” 嗎?
1920 年代德國數學家 David Hilbert 準備為數學訂立一條可以驗證所有”真理”的規則,但Kurt Gödel 証明了此目標並不可行: 「 任何無矛盾的公理體系,那怕只是包含初等算術的陳述,必定存在一個用這組公理不能判定其真假的命題。」也就是說,“無矛盾” 和 “完備(適用於所有情況,包括自己)” 是不能同時滿足的。這就是 “哥德爾不完備定理” 。
有人就認為因為 “哥德爾不完備定理”適用於任何公理體系,所以機器不能跳出體系而另行創建體系進行思考。但亦有人指出 “哥德爾不完備定理”適用於機器亦適用於人腦,故機器亦能思考。
參考
1《Gödel,Escher,Bach: an Eternal Golden Braid》(1979) Douglas Hofstadter (Pulitzer Prize 1980)
2《Gödel, Escher, Bach: A Mental Space Odyssey》
http://ocw.mit.edu/high-school/humanities-and-social-sciences/godel-escher-bach/
3 Wikipedia