SENSE隨筆140605
統計學淺談:  阿特蘭大作弊事件
執筆人：蟬

2009年美國阿特蘭大巿報章報導，巿內某公共學校呈報的 “州立公開試CRCT”成績有作弊嫌疑。 州立調查局介入調查，發現巿內56間公共中學當中竟有44間涉嫌作弊，共牽涉178位教職員，皆為教師和校長。 其後更發覺作弊行為可能早於2001年經己發生，教師和校長涉嫌將學生答錯之試題修正才遞交當局。

這樁作弊醜聞有趣的地方，是在教職員大範圍牽涉而又沒有人其他學校舉報的情況下，作弊是如何被揭發的呢？

改過自身也有錯？
在阿特蘭大醜聞中，最先引起人注意的是試卷有大量「由錯改對」的情況。 當然，學生在覆卷的時候發現錯誤並修正是很合理的， 甚至原本答對了而「由對改錯」的也大有人在。 事件中引人注目之處，正於阿巿 “由錯改對”的行為比全州高出很多。 據分析數據的官員形容，這種情況出現而純為巧合的機率，約略等於七萬名在巨蛋球場看球賽的觀眾恰巧全都高過七呎。 J

雖然該種 “非常情況”不能百分百確定存在作弊— 實際上統計無法百分之百確定任何事情，*** 但卻有足夠理據去發起調查。

對於外行人來說，要理解如何以統計去“偵查” 異常數據似乎相當困難，當中牽涉一大堆專業術語。 但統計學中某些基本方法和理論，對於判斷日常生活的事理卻有不少幫助。

〈尋找失落的旅遊巴士〉
假設大家都知道甚麼是 平均數mean。現在試看以下的例子。

城中正同時舉行兩個美食展覽： “香腸展覽會”和 “有機蔬菓展覽會” ，兩個展覽會均極受海外朋友歡迎。 會方為疏導數千名海外參觀者，特意提供機場往返會場的穿梭巴士服務。 作為工作人員，主管突然致電給你說其中一輛滿載有機蔬菓展訪客的旅遊巴失去聯繫，要你幫忙把它尋找出來。

當你盤算如何著手之時，發現面前正有一輛載滿外籍乘客的巴士，可是由於語言不通，無法得知他們是否有機展覽的訪客，而主管給你唯一的資料是「全體海外參觀遊客的平均體重為140磅。」 手足無措的你決定替車上60名遊客量度體重（不知哪來的秤），得到的平均體重為170磅。

不懂統計的人看到這裡，大概也可以斷定這輛巴士並非有機展覽的，原因是遊客的平均體重太重了。但我們要如何系統地把這個判斷表達出來呢？

要以統計角度進行分析，我們先要弄清一些基本概念。 在例子中，主管給出的數據是以所有遊客為對象的，是分析中的母體population，包括統計對象所有成員。

舉例：香港人口普查的母體便是香港所有居民，而被選中接受普查的居民便是樣本sample。
越具代表性的樣本，便應該越與母體相似。***
如果巴士上的是有機展覽的遊客，則車上遊客的體重應該與母體相似。

〈充滿差別的成員〉
為了讓這個分析的目標更科學，我們先定下一個假設：旅遊巴士上的乘客都是有機展覽的遊客。

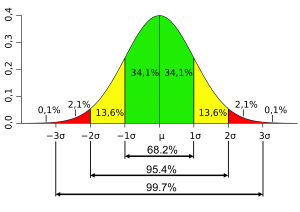
大家也知道，即使母體的平均體重是140磅，遊客個別體重的差別卻可以很大。統計學以標準差standard deviation (SD)去表達一個母體內成員的差異。 上面例子中，資料顯示母體的標準差為9磅。 意思是成員的體重很大機會在一個標準差內(131-149磅)，而更大機會在兩個標準差內(140±18)；而幾乎沒有成員會在3個標準差以外。 這種成員分佈的形式，便是著名的「常態分佈normal distribution。」
（註：計量上的表達為68.2%在SD內，95.4%在2SD內和99.7%在3SD內。）

如果巴士上的乘客就是一個從母體的抽樣，即使隨機抽樣的成員及體重分佈不一樣，他們也應該有相當的相似度。 你替巴士乘客量度體重時也順便把標準差12算出來。 所以母體和巴士乘客的體重分佈(1SD)範圍便分別為131-149及158-182，兩者並沒有交集。

好了這似乎給出了很強的證據了吧？但似乎抽樣時的偏差也會造成這個狀況。 既然這樣，我們便唯有引入「中央極限定理」了。

〈中央極限定理Central Limit Theorem〉
Def. 中央極限定理指出，任何母體的樣本平均數會圍繞著母體平均數約略形成一個常態分佈。***

將定理運用在我們的例子上，大概便是這樣：

將每輛接載有機展覽的巴士(隨機樣本)上乘客的體重計算出一個平均數，由於每輛車的成客都不同，所以平均數並不一樣。但大多數樣本的平均數將非常接近母體平均數。

中央定理指出所有樣本的平均數將以母體平均數為中心以並以常態分配， 無論母體的分配形狀為何。*****

要了解樣本平均數的常態分配如何，我們要引入一個新的概念：「標準誤standard error」。標準誤是用來衡量樣本平均數的分佈性的。*** 而之前提到的標準差則是用來衡量母體的分佈性。 所以我們可以進一步說：標準誤便是樣本平均數的標準差！

標準誤越大，樣本分佈的範圍越廣。 母體的標準差越大，則合理地個別樣本的平均數差異也越大；而樣本規模越大，則個別樣本的平均數差異也越小。 標準差的公式為S/√N，當中S為母體的標準差，而N為樣本的規模。

例子中母體的平均數為140磅，標準差為9磅；旅遊巴士乘客的平均體重為170磅，樣本規模為60。以此得出標準誤為1.16。

170磅分佈在母體平均體重的26個標準誤內。機會之低難以數字表達，要落在7個標準差內的機率大概等於10.7億年出現一天的事件。 所以，旅遊巴士上的乘客來自有機展覽的機會率幾乎是零。 我們可以挺肯定地推翻這個假設，因為我們的運氣應該不至於那麼壞。

參考：
《聰明統計學的13又1/2堂課》
《Naked Statistics: Stripping the Dread from the Data》(2013)  Charles Wheelan