SENSE隨筆141203
偏好排序法Preferential Voting System（PVS）3之2
朝日執筆：選舉簡介系列（五）
既然SMS可以引入「排序Preferential」概念，從而「進化」為IRV，那麼「排序」方式是否也可以加入PR選舉之中呢？當然可以。 「比例代表制PR」的理念是讓各政黨可以按照其在社會上的支持度獲得議會中「相應比例」的議席。為什麼不能將選民的偏好也「按比例反映」呢？因此就有了「可讓渡單票制Single-Transferable Voting（STV）」。
之前介紹過的「最大餘額法Largest Remainder（LR）」和「最高均數法Greatest Average（GA）」，都是由政黨預先排好一份名單，選民只有一票，只能在各份「餐單」挑選其一。 為什麼選民就不能有「跨黨派」的選擇，而定必要捆縛式地取捨呢？在這個時候，STV幫到你！
STV適用於多議席選區，正如上面所說，也是「比例代表制」一種，而且STV與「最大餘額法Largest Remainder（LR）」也有相似之處，因為它也是一種處理「超過某數額Quota後的餘額」的方法。 在之前介紹LR時，我們介紹過「黑爾數額Hare Quota（HQ）」，即該選區的總有效選票，除以所需競逐的議席數。這是各種在選舉中採用的「數額」概念中，最簡單易明的一種，但卻並非最常用的一種。 大多數STV選舉中使用的都是「特立數額Droop Quota（DQ）」，所以這裏要為大家介紹一下。
首先問一個簡單數學邏輯問題。假設在實行PR制的選區內，共有四席可供N張名單競逐。那麼任何一張參選名單「甲」，究竟最少要拿到多少個%的支持，才穩拿一席？25%？這正是HQ的邏輯！
但再想清楚，其實甲名單拿到20%再多一票，已能肯定不會同時有另外四張名單的得票比它高！**** 也就是甲名單已經能夠穩拿一席了！對嗎？這個Def. 「有效票總數 ÷ (總席數 + 1) +1票」，就是「特立數額Droop Quota（DQ）」了！
現在以較為典型的澳洲參議院選舉作為藍本解說STV。
在STV中，候選人皆以個人身份參選。假設一個選區要選出N個議席，選民就必須在選票上按照屬意的順序，在選票上劃出N個選擇。點票時先點算各候選人所獲的的「1選」，若有任何一名候選人甲獲得的「1選」已超過DQ，即獲得議席。然後甲的選票會按照票上的「2選」，先打一個折扣，然後再撥給相應的候選人。***** 為什麼要先打一個「折扣」呢？這是因為甲「用了這些票」當選後，這批選票中的每一個「2選」就不再值「一票」了。
舉例說某選區要選4個議席，總有效票數為100,000票，DQ就是100,00票 ÷ (4 + 1) + 1 = 20,001票。 假設甲獲得了40,001「1選」票，超過了DQ，他自然順利當選了。 接著那40,001票就會在按票上的「2選」分配予其他相應的候選人。然而，由於甲已「使用了」那40,001票中的20,001票來當選，所以當這40,001票分配予「2選」候選人時，每票就不再值「一票」，而只值(40,001 – 20,001) / 40,001 ≈ 0.5。這40,001「2選」票就以每票值「0.5票」的方式撥入相應的候選人，然後作第二輪計票。***
假設有候選人乙本來有19,001「1選」票，而甲40,001「1選」票中，其中有20,000票的「2選」是乙，「折算」成20,000票 X 0.5 = 10,000票（Def. 凡「未用過的」或「與1選票等值的」票，下面稱為「完整票」。）撥給乙。 乙得到這「兌換出來的」10,000「完整票」，加上原來自己的19,001「1選」票，共有29,001「完整票」，超過了DQ，又獲得了一個議席。 接著，乙自己這「用過的」「1選」票同樣以(29,001-20,001) / 29,001 ≈ 0.31的票值，分配給那19,001票中的「2選」候選人。 而那20,000票「1選甲、2選乙」的選票，由於已經「再使用過」，故也會按0.5 X 0.31≈ 0.155的票值，分別再撥給這20,000票中的「3選」候選人。然後，再進行第三輪計票。如此類推，直到議席分配完畢為止。
如在一輪計票中，沒有任何一名候選人達到DQ，則將此輪計票中「完整票」最少的一位候選人庚淘汰，並將其選票按票上的「下一個最先選擇」撥予相應的其他候選人。然而，由於庚並沒有當選，故他的「1選票」並沒有「使用過」，因此每票均可按「原值」分配給各「2選」候選人。然後，再進入下一輪計票。
下文嘗試用圖表方式舉例說明STV的具體運作。 假設某選區H要以STV選出四個國會議席，而該選區共有甲、乙、丙、丁、戊、己、庚七名候選人參選。 也就是每名選民都要在七名候選人中選出四名，並以1、2、3、4將四名候選人排序，共有840種可能。 總有效票數為100,000票。為求簡化，下面不會列出全部數據。
總票數：100,000票
第一輪計票中，只有甲的得票（40,001票）超過「DQ=20,001」，因此甲先獲得一席。由於甲「使用了」其40,001票「1選票」中的20,001票以獲得席位，故這40,001票將以(40,001 – 20,001) / 40,001 ≈ 0.5的比值按票上的「2選」撥入相應候選人，以進行第二輪計票。
以下為甲的40,001「1選票」，按其「2選」撥入後，進行第二輪計票的過程：
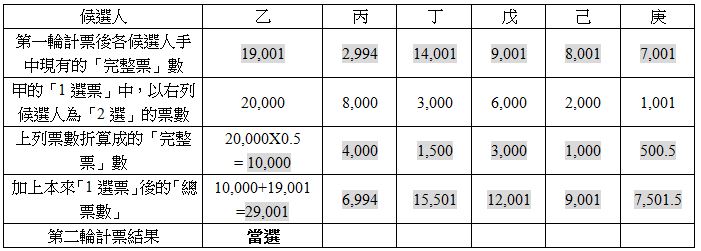乙得到29,001「完整票」，超過DQ，獲得一席。 被乙「使用過」以獲得議席的「乙1」選票，會以(29,001-20,001) / 29,001 ≈ 0.31的票值，按照票上的「2選」分配予相應候選人。而該20,000「甲1乙2」的選票，由於已「使用過兩次」，則會以 [(40,001 – 20,001) / 40,001] X [(29,001-20,001) / 29,001] ≈ 0.155的票值，分別再撥給這20,000票中的「3選」候選人。 至於之前「甲1」選票中以其他五名候選為「2選」的20,001票，由於還沒有「使用第二次」，故仍會以(40,001 – 20,001) / 40,001 ≈ 0.5的票值，保留在該五位候選人手中。
以下為將甲及乙當選後的「剩餘票值」，分別撥入其他相應候選人後，進行的第三輪計票過程：
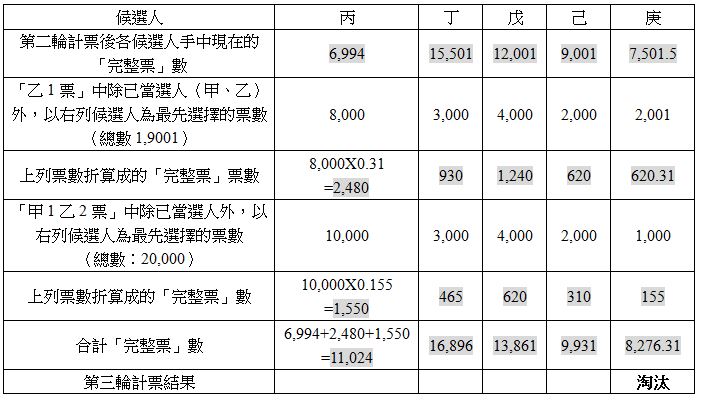
經過第三輪計票，並沒有一名仍在競逐中的候選人，所得的「完整票」數高於DQ，故將本輪計票後所得「完整票」數最低的候選人庚淘汰，並將其「名下的票」按票上除已當選人（甲、乙）外的最高選擇，分配予其餘候選人。 請注意，由於在第三輪計票中並沒有選票「被使用」以獲得議席，故此在第四輪中的所有選票（包括「庚1票」、「甲1庚2票」、「乙1庚2票」、「甲1乙2庚3票」……）都不用再「打折扣」，而仍會按第三輪計票時的票值作分配。***
以下為將庚淘汰後，其「名下的票」作出「相應讓渡」後，進行的第四輪計票過程：
丁得到21,097.5「完整票」，超過DQ，獲得第三個議席。被丁「使用過」以獲得議席的「丁1」選票，會以(21,097.5-20,001) / 21097.5 ≈ 0.052的票值，按照票上的「2選」分配予相應候選人；而其他「甲1」、「乙1」、「庚1」的選票，也會以「被誰用過」和「用過多少次」計算出相應的比值，撥入票上「下一個選擇」的候選人，然後再進入第五輪計票。 這個模擬演示到了這裏，所有需要解釋的情況和要素都已經出現過，可說 ‘精華已竭’了。
經過第四輪計票，丁取得第三個議席，而最後一個議席的爭奪，則由戊領先。大家應會發現，其實丙除了「1選票」外，以後在「每一級選擇」的票數都比戊要多，「（不分優次計的）總票數」也比戊多。 而越往後輪次的計算，每票的「價值」就會越低，逐漸趨近於0。 故此，即使在下一（幾）輪的計票中，絕大部分選票的「次一優選」都偏向丙或己，也很難逆轉二人的落後形勢。最後的一個議席，如無意外還是會落在戊的手中。這說明了「選擇次序」的重要。