讀書札記170605
《不當行為》(三十)我諗你一定以為我係咁諗你點諗我點諗你……
朝日執筆
相比於同時代的其他經濟學家,凱因斯對「金融市場」有更「切身」的洞見。「薯仔堆滿辦公室」的故事,大概只是一個「都市傳說」。然而,他長期擔任「劍橋大學國王學院King’s College, Cambridge」的「基金經理」,造出亮麗成績,並首倡把「捐款」用於「證券投資」(以前只能放在銀行「收息」),這些可不是蓋的呀!
早在「效率市場假說Efficient-market Hypothesis」被提出的三十幾年前,凱因斯就認定,股市並不是一個「效率市場」。他舉了一個經典的例子—雪糕公司的股價,在夏季竟然會隨產品銷量增加而上升!這顯然是不合理的。因為「寒來暑往,秋收冬藏」,這些是最清楚不過的「公開資訊」,因此,股價反映的應該是公司長期價值。「效率市場」對「明知必然會發生的事情」(例如雪糕夏天銷量會上升),應該即時(例如在冬天甚或「盤古初開之日」)就作出了反應,而不會等到事情真的發生時(例如某年夏天)才作出反應。
凱因斯的觀察和評論,到了今天依然有效。他所描述的現象,到了現在仍不少見。例如不少零售或航運股,年復一年地在感恩節至聖誕節期間,股價都會上升。到了「業務淡季」,又跌回來。
「效率市場假說」的其中一條重要支柱,是認為在市場出現「不理性行為」(例如定價「過高」或「過低」)時,自然會有「聰明錢Smart Money」與其對做,從而把市場「擺平」,重回正軌。不過,凱因斯卻認為那些「行家」們,其實更熱衷於乘著「不理性繁榮」的浪頭,而非與之對做,因為他們選擇「最佳股票」的標準,並不僅僅是「憑良心」而已。
情境30a:本年度「鄉講小姐」三甲,將由全城觀眾投票選出。得票最高的三位佳麗就是優勝者,而投票選擇與比賽結果相同的觀眾,將有機會獲得「豐富禮品」。最簡單的想法,就是每個觀眾投給自己認為最漂亮的三位佳麗。然而,如果每個觀眾都一心以那些「豐富禮品」為目標,投票時就不一定會(或者「一定不會」)投給自己心目中認為最漂亮的三位佳麗,而會投給他認為其他觀眾會最喜歡的三名佳麗。我們現在來到第三個層次,就算不是全部,也總有些「城府較深」的觀眾,明知其他觀眾會有上述的想法時,會盡量去預測普遍觀眾會怎樣去預測普遍觀眾認為最美的三個。之後當然還會在第四、五、六,以至更多層次的預測。
凱因斯用這個「選美情境」,來比喻投資者在金融市場中的選股策略,實在非常精彩!他們想的不是「哪隻股票會升」,甚至還不是「普遍人認為哪隻股票會升」,而是「普遍人認為普遍人會認為哪隻股票會升」,甚至是「普遍人認為普遍人認為普遍人會認為……
如果一直推下去,會有什麼結果呢?「股票」或「佳麗」到底「有幾靚」?「美貌(或智慧)」畢竟難以數字量化。於是,Thaler又想到了一個「數字競猜遊戲」。
情境30b:請從0至100之間猜一個整數。所猜數字,最接近全體參賽者猜測數字平均值的三分之二的,就是優勝者。
舉例說,如果只有三個參賽者,分別猜18、27、36。三人所猜數字的平均數為27,27的三分之二就是18。所以,猜18的那位玩家就是優勝者。
我們現在一起玩一局,在繼續讀下去之前,請你就先猜一個數字。到最後一起看Thaler實驗中的優勝者,跟你猜的到底有多接近。朝日知道,作為野人一員或者掌門友好的你,是如何的「聰明」。因此大概也猜到,你在作出猜測之前,應該會有問題想問。不過還是稍後才回答你吧!就按現在的資訊,先猜個數字吧,投入感大點才好玩嘛!
這種「個個都咁醒」之餘,又「個個都知道其他人好似自己咁醒」的場面,最適合用「囚徒式互相猜度模型」來分析。
由「零層次」開始,如果所有玩家都是「好Pure好True」的玩家,他們只會以「隨機」的方式猜數字,於是所有人猜的「平均值」就是50了。
「第一層次思考者」會這樣想:「班友邊有腦架?實係『Hea估』啦!這些『零層次思考者』隨便猜出來的『平均值』會是50,那我就猜33(即50的三分之二)吧!」
「二層人」會想:「班友實會『懶醒』,以為其他人都係『傻嘅』。因此這些『一層人』會猜33,所以我就猜22!」
「三層人」會想:「稍微有啲腦都應該知發生咩事啦!所以班友一定以為自己已經好英明咁洞悉咗『一層人思考模式』。他們會沾沾自喜地猜22,我就『黃雀在後』猜15!」
……
這樣往下還可以再推幾層,但並不會沒完沒了。套用一個學術名詞,這個遊戲的「納殊平衡Nash Equilibrium」(參閱第廿二集)是「0」(或者「1」)。因為這已是反覆互相猜度至「沒有進一步思考空間」的狀態了。
好了!你在遊戲開始前不是有問題想問嗎?作為本會會友,SENSE澎湃的你必然第一時間就會想到,在作出猜測之前,首先必須知道對手到底是誰?如果其他參加者都是些「很傻很天真」兼且「好打意」的「玉女歌手」,你猜33大概也就差不多了;如果是一般社交聚會,也許22還是挺靠譜的;不過,若果所有參加者都是博奕論專家(或「邪惡的」野人會眾),那麼就沒有比猜0更合理的選擇了!
這個「數字競猜」遊戲和凱因斯的「選美競猜」,在結構上是一模一樣的,分別只是「美」畢竟比較抽象,但「數字」則易於量化。這個實驗最初是德國經濟學家 Rosemarie Nagel發明的。不過Thaler卻在因緣際會之下,得到一個向「菁英」實驗的機會。Thaler說服了英國《金融時報Financial Times》為他舉辦這個競猜遊戲,並得到英航贊助兩張倫敦來回紐約的商務機票作為獎品。
現在遊戲的「蹊蹺」也告訴你了,對手也告訴你了,無獎問答遊戲正式開始。面對著這些《金融時報》的讀者群,你會猜多少?
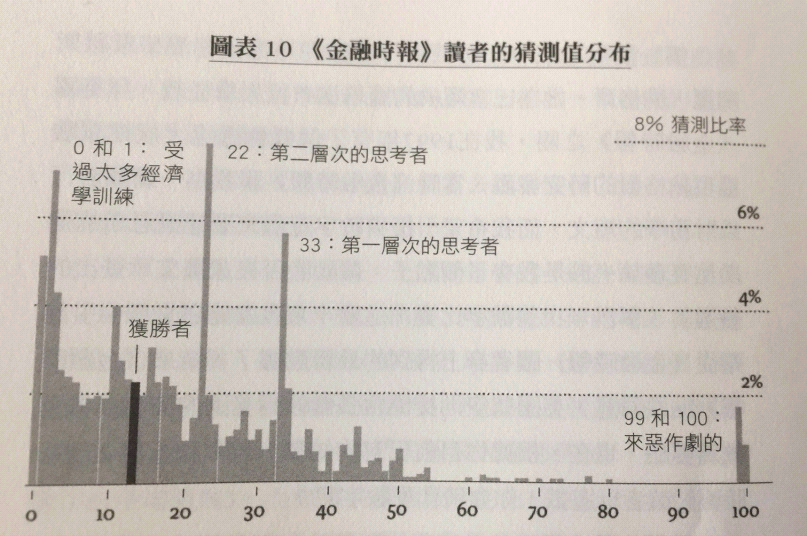
不拖戲了,直接就告訴大家,得獎的數字是「13」!所有讀者猜測的數值分佈見圖表10。
毫不意外,很多「讀過下書」的《金融時報》讀者,都知道「納殊平衡」是「0」。不過,最多人猜的卻是「1」 。Thaler歸咎於自己題目字眼上的「語病」:「從0至100之間」,有可能令人理解為選擇並不包括「0」和「100」。當然,也有可能是這些「猜1者」知道「傻瓜」總是「老是常出現」,即使在《金融時報》的讀者群中也一樣。因此,他們預留了少許的「緩衝帶」。
預留「緩衝帶」的想法是正確的,問題只是留得太少。因為結果顯示「一層人」和「二層人」的數量非常多。至於那些「99」和「100」的,很明顯是惡作劇,但也不能排除是「黑幕造市」,正如真實股市中的「虛假交易」一樣。可幸這些「異常交易」,只是把「得獎數字」由「12」微微拉高至「13」。
以上的數字大約展現了《金融時報》讀書的思考精密程度,看來也不全然是「純理性人」。他們當中大概不少都是金融業界的「行家」。有些基金經理不諱自己是「成長型投資者Growth Investor」,意思就是他們不理會股價貴不貴,只在意其股票還會不會上漲。另一類基金經理會自稱為「價值型投資者Value Investor」,聲稱自己會以「價值被低估的便宜股票」為目標。
不過,如果明知某隻股票還會繼續跌,就算價格如何便宜(被低估),大概也不會有人想買吧?說到底,關鍵還是要買一隻「其他投資者不久後就會買進」的股票吧!正如凱因斯的「選美競賽」一樣,與其說是選「股票」(靚女)本身,不如說是「我諗你一定以為我係咁諗你點諗我點諗你……會㨂邊隻股票(靚女)」的「猜心遊戲」。
「長期投資」?容許朝日不厭其煩地,再和各位重溫一次經濟學界巨人(6呎6吋,與米高佐敦一樣高)凱因斯的「不朽名句」:
「In the long run we are all dead!」
吓!我知,我梗知啦!你唔係「坐艇」,你係「長期價值型投資者」吖嘛!
30集關鍵字:
效率市場假說Efficient-market Hypothesis
聰明錢Smart Money
選美競猜/猜數字遊戲
(無限)多層次思考
納殊平衡Nash Equilibrium
成長型投資Growth Investing
價值型投資Value Investing
《不當行為》Richard Thaler著/劉怡女 譯
