SENSE隨筆140317
懦夫博弈： 謝林Schelling博弈論淺談
執筆人：蟬

〈懦夫博弈〉
1961年栢林危機，大批東德人逃向西德，局勢緊張。 蘇聯領導人 赫魯曉夫Khrushchev威脅要開戰。 當時美國總統 甘乃迪 J.F. Kennedy對赫氏的挑戰擺出強硬的姿態，並公開宣布：“我們已經做出承諾，攻擊西柏林將被視為攻擊我們全體。和平還是戰爭主要看蘇聯的選擇，而不是我們的選擇。”

現任新加坡傳訊部長的Janadas Devan曾以著名的「懦夫博弈 The game of chicken」去比喻當時這種狀況。 懦夫博弈是指兩名博弈者筆直地向對方驅車衝刺，誰先動搖並改變方向便是懦夫。 如果兩人都堅定不移，雖則沒人丟臉，卻都丟了性命。 假如死不如生，則最佳結果似乎是兩人同時轉向。

諾貝爾經濟學得獎者 謝林Thomas Schelling 認為博弈者的最佳策略是：猛踩油門， 並把車上的方向盤摘下，伸出窗外向對手揮舞，並大聲喊道：“喂兄弟，我這輛車沒法轉彎！”***
這策略正正是謝林在栢林危機時給甘乃迪的建議。

〈權衡形勢〉
謝氏在60年代開始涉足策略研究，文章《論討價還價Essay on Bargaining》以一套日常的詞匯套上策略定義而廣受歡迎。 謝氏當時為耶魯大學的經濟學教授，身兼軍事智庫組識Rand Corporation的成員。

謝氏認為討價還價包括了 自我約束、破釜沉舟和減少選項的能力。*** 為了更清晰了解討價還價的策略如何以博弈論的角度詮譯，我們先看一下決策理論常用的工具：收益矩陣Payoff Matrix。

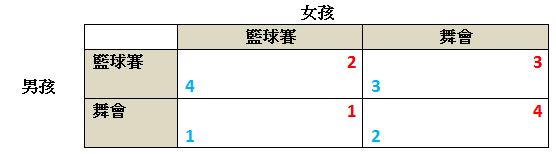
舉例：愛籃球的男生與愛舞會的女生互有好感，期望能在周末約會。 但周末剛好有一場年度最重要的籃球賽和最盛大的舞會同時進行，男生與女生皆想參加相應的活動。要了解周末兩人的最佳選擇，需先參考兩人的偏好排序：
男生偏好序
1) 一起看球賽
2) 男生看球賽，女生去舞會
3) 一起去舞會
4) 女生看球賽，男生去舞會
女生偏好序
1) 一起去舞會
2) 男生看球賽，女生去舞會
3) 一起看球賽
4) 女生看球賽，男生去舞會

兩人的偏好建構的收益矩陣為：

圖中藍字為男生的偏好收益，以4為最佳；紅字則為女生。

在矩陣中可以清楚看到，對男生來說，第1行row的選項明顯較第2行為佳，即男生看球賽，無論女生去哪也比男生去舞會為優。所以對男生來說，選擇看籃球賽（第1行）是 佔優策略dominant strategy。*** 而對女生來說，則去舞會（第2列）為佔優策略。
Def. 「佔優策略」是指無論對手的策略為何， 該策略始終為博弈者的最佳選項。***

在兩名博弈者都擁有佔優策略的情況下， 雙方佔優策略交集的地方便是 自然結果，並且是一種「納什平衡Nash Equilibrium」。*** 在這例子中，自然結果明顯是男女生各自各精采。

〈威脅與承諾〉
在日常生活中，人們討價還價時會不自覺地用上某些策略， 但若要清楚定義策略和列舉適用的狀況則相當困難。 謝氏的有趣研究成果便是將通用的策略系統地以日常語言表述出來。

舉例：兒子不希望繼續升學，與父母則意見相左。 父母並不富有，但知道兒子很喜歡汽車，所以寧願給兒子買一輛車“收買”他繼續升學。
以兒子和父母的偏好建立的收益矩陣為：

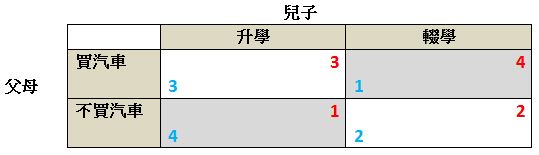
如沒有任何承諾，則右下格為自然結果：父母不想花錢而兒子不想升學。

父母為了“收買”兒子而作出「承諾」，如果兒子升學便給他買汽車。 承諾排除了收益矩陣中右上格和左下格的可能性，如果兒子因而選擇升學，則父母和兒子的“收益”便可同時增加，代價是父母需要花錢購買汽車。***

Def. 策略研究中，「承諾」包括兩個原素：
1. 博弈者作出承諾，就是宣佈他將做出符合對手可察覺利益的決定；
2. 策略成功通常需要付出高昂的代價。*****

面對同樣情況，父母還有甚麼策略可以運用呢？「威脅」是也。
舉例：父母把蘿蔔換成鞭子並對兒子說：如果你退學，我們便把家裡的互聯網服務取消。 父母和兒子其實同樣沉迷facebook和網遊，把互聯網服務取消將令大家都相當痛苦。
此際收益矩陣可表達為：

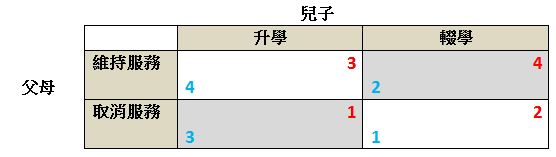
父母的威脅排除了右上格和左下格的可能性，令兒子必須重新考慮。 若兒子選擇升學，父母的收益便可提升兩級。

Def. 策略研究中，威脅包括兩個原素：
1. 博弈者表示有意作出原先不會作出的選擇；
2. 策略失敗時博弈者需要付出高昂代價。

威脅另外還有一些特性：
a. 為使威脅有效，它們常常伴隨承諾**；
舉例：如果兒子輟學父母便取消互聯網服務，暗含著如果兒子升學便維持服務。
b. 為使威脅有效，做出威脅者在博弈中不能首先行動。***

參考
《哈佛大學的博弈論課》( 2013) Robert Dodge
《Schelling’s Game Theory: How to make decisions》